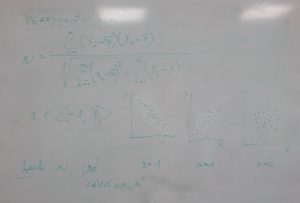Category: statistika

Jejich podstatou, stejně jako u lineární regrese a jednofaktorové ANOVA, je rozdělení varibility závislé proměnné (kterou je vždy poměrová proměnná), na části, které jsou schopny vysvětlit jednotlivé použité nezávislé proměnné (které mohou být podle modelu poměrového až nominálního charakteru) a část těmito proměnnými nevysvětlitelné.

Software určené ke zpracování dat jsou obvykle nastaveny i k jednoduchému ovládání počítání složitějších úloh, než je ANOVA jednoduchého třídění (k zopakování tabule).

Pro zopakování základní info k One-way ANOVA.

Pokud máme na straně vysvětlovaných proměnných jedinou proměnnou, patří různé typy ANOVA (vedle regresí) k nejčastěji používaným nástrojům řešení problémů pro factorial i nested design pokusů a sběru dat. Jde samozřejmě o případy, kdy mám více než jeden kategoriální prediktor – abychom se ve výsledcích byli schopni “rozumně” orientovat je dobré, aby faktory měly jen dvě úrovně (popř. 3) a aby těch faktorů určitě nebylo víc než 4.

Design sběru dat pro různé modely ANOVA.

U faktoriálního designu (na tabuli) lze v základu použít faktorovou ANOVA, pokud počítáme s interakcemi = předpokládáme, že vliv sledovaných kategoriálních proměnných (faktorů) není pouze aditivní – tedy, že kromě vlivu měřených proměnných, existuje i nenáhodný vliv kombinace těchto faktorů na variabilitu hodnot sledované proměnné. Je-li vztah čistě aditivní, pak používáme ANOVA hlavních efektů.

Pro klasická faktoriální data, aby je šlo “jednoduše” hodnotit pomocí ANOVA, platí:

• počty úrovní u faktorů se mohou lišit
• počet opakování v každé kombinaci by měl být stejný, pokud není, lze výpočty dělat, ale obvykle se speciálním nastavením – experimenty plánujte vždy se stejným počtem opakování!!!!!!!!!
• pokud nemám opakování, nemohu použít Factorial ANOVA, jen Main Effect ANOVA, protože není kde brát variabilitu pro průměr v každé kombinaci úrovní faktorů

Faktorová (factorial) ANOVA

Testujeme vliv dvou a více kategoriálních faktorů a současně vliv vzájemné kombinace těchto faktorů (= neaditivitu) na závislou proměnnou. Suma čtverců (SS), počet stupňů volnosti (DF) i variabilita (MS) se pro faktory počítá identicky jako v One-Way ANOVA (tedy jako SSG, DFG a MSG). Reziduální MS a SS se počítají taktéž stejně jako u One-way ANOVA, DFE je pak dán součinem počtu úrovní všech faktorů a počtu měření v kombinaci úrovní faktorů (ten poslední se obvykle značí r) sníženého o 1. Výpočet interakce faktorů je pak náročnější a základem variability je rozdíl průměru hodnot naměřených v dané kombinaci úrovní faktorů a jeho očekávané hodnoty. Tato očekávaná hodnota se vypočítá jako součet průměrů úrovní faktorů pro danou kombinaci (= u Two-way ANOVA jde průměr řádku a průmer sloupce dané kombinace úrovní faktorů) od nichž odečtu hodnotu celkového průměru. Rozdíl reálného průměru v kombinacích úrovní faktorů a očekávaného průměru v dané kombinaci faktorů pak musím násobit počtem měření v dané kombinaci úrovní faktorů. Počet stupňů volnosti je pak dán součinem úrovní faktorů, snížených 1 u každého faktoru.

Speciálním případem faktorové ANOVA je dvoufaktorová (dvoucestná) ANOVA, kterou umí i MS Excel (video). Učebnicovým příkladem (Lepš, 1996) jednoznačně neaditivních faktorů je test vlivu kombinace zálivky a hnojení na růst rostlin. Ve společenských vědách mohu třeba sledovat současný vliv pohlaví a věku (vyjádřený ve věkových kategoriích) na hodnocení atraktivity výstavy zbraní v zámecké expozici.

• Příklad z přírodních věd: hodnotíme vliv dvou dvouúrovňových proměnných na druhovou pokryvnost (předpokládáme splnění požadavku na zcela náhodné rozmístění ploch). Těmi faktory jsou minerální bohatost a množství živin. Nejprve na příkladu Drosera rotundifolia a následně Carex lasiocarpa.

Factorial ANOVA pro Drosera rotundifolia.

Factorial ANOVA pro Carex lasiocarpa.

ANOVA hlavních efektů (Main Effect ANOVA)

Používám pro testování pouze hlavních efektů – a priori na základě znalostí problematiky předpokládám aditivitu, tedy vzájemnou nezávislost sledovaných faktorů). Další možností je případ, kdy jsem ve Factorial ANOVA nemohl vyvrátit nulovou hypotézu o neexistenci vazby mezi faktory – nicméně platí, že to, že jsem nemohl zamítnou hypotézu o významu aditivity, ještě neznamená, že jsem potvrdil aditivitu – viz nulové hypotézy.

Při použití ANOVA hlavních efektů veškeré odchylky od aditivity považuji za náhodné a tyto odchylky se stávají součástí celkové variance – SS pro celkovou varianci se vypočítá jako součet reziduální SS (=SSE Factorial ANOVA) a interakční SS (vypočítané stejně jako u Factorial ANOVA), stejně tak DF celkové variance v Main Effect ANOVA je součem DFE a interančního DF. Praktické použití ve STATISTICA jsme si ukázali v předchozí části.

Pevné (fixed) versus náhodné (random) faktory

Pro použití ANOVA, do jejichž modelů vstupuje více faktorů, je významné rozhodnutí, jestli testuji vliv faktoru pevného nebo náhodného. Toto rozhodnutí dělán na základě podstaty dat vzhledem k výzkumné otázce a tedy stanovené nulové hypotéze. Pokud mě zajímá konkrétní úroveň faktoru, pak se jedná o faktor pevný, pokud je tento faktor jakýmsi obecným náhodným případem a mě zajímá na obecné a nikoliv “věcně” konkrétní úrovni, pak je náhodný. Rozhodování je často obtížné a odvíjí se od konkrétní situce nastoleného problému a jeho řešení, přesto lze uvést jakousi všeobecně platnou radu: pevné jsou obvykle faktory, které vysvětluji = jsou vlastním předmětem mého výzkumu, náhodné jsou faktory, které nějak souvisejí s designem pokusu (jsou náhodné a nikoliv vysvětlované, a to, co obvykle testuji, je zobecnění a nikoliv rozdíly mezi konkrétními místy, kde jsem pokus provedl).
Příklad mám dva zásahy a kontrolu, tedy 3 typy zásahu celkem, a budu v experimentu každý zásah opakovat 3x. Celkem mám tedy 9 měřených ploch. Aby to bylo naprosto správně, pak mohu udělat v podstatě tři základní věci: (1) použít (zcela) náhodné rozmístění ploch, (2) úplné znáhodnělé bloky, nebo (3) latinský čtverec. V každém z těchto případů musím použít jiný typ nastavení ANOVA – pro náhodné rozmístění (bod 1) použiji One-way ANOVA (faktor je typ zásahu = tři úrovně), pro úplné znáhodnělé bloky (bod 2) použiji Two-way ANOVA, kde zásahy budou fixed, bloky random, model je main effect, pro latinský čtverec budu muset použít Three-way ANOVA, kde fixed budou zásahy, ale pořadí plochy v řádku bude jeden random effect a pořadí plochy ve sloupci bude druhý random effect.

S tímto je problém ve STATISTICA, pokud používáme rychlého průvodce ANOVA v přímé nabídce Statistics – v nastavení random versus fixed jinak než otevřením syntax editoru nelze. Takže pokud chcete použít jen průvodce a hodnotit Factorial ANOVA nebo Main effect ANOVA, pak nemůžete použít jejich nabídku a musíte zvolit jeden z následujících postupů:

• na kartě Statistics položku Advanced models a v ní Variance components. V průvodci pak na záložce Quick zvolím požadované proměnné (všimněte si, že tam lze navolit i kovariátu – čili tento nástroj použiji i pro složitější designy ANCOVA), na kartě Model pak na druhé volbě volím jestli interakce mají bít fixed nebo random (zde si všimněte, že kromě factorial design lze níže nastavit i nested design).
• další a v drtivé většině případů šťastnější volbou je volit Advanced models – General linear a na jejich kartě zvolený typ ANOVA (factorial, main effect, hierarchical) nebo dole obecně General linear models. V dialogu nastavení na kartě Options mám nově volbu nastavení, které efekty mají být náhodné. Také zde lze nastavit poměrovou spojitou kovariátu. Přehled nastavení pro měření provedené na pokryvnosti Carex lasiocarpa s nastavením obou efektů jako random je na videu.

Nastavení náhodných faktorů ve STATISTICA.

Matematický rozdíl v pevných a náhodných efektech – výsledky pro nastavení pevných a náhodných efektů se liší neboť se liší výpočet F-testu. V čitateli zůstá v obou výpočtech MS faktoru, ale ve jmenovateli je pro pevné efekty reziduální průměrný čtverec (jaku u One-way ANOVA), ale u náhodných faktorů je ve jmenovateli interakční průměrný čtverec.

Mnohonásobné porovnání – podobně jako u One-way ANOVA, kde jsou tři a více úrovní grupovací proměnné, i zde lze pomocí post-hoc testů identifikovat “co se od čeho liší.” Ve STATISTICA vypadají karty Factorial i Main effect ANOVA stejně jako u One-way ANOVA. Pokud použijete nástroj Variance components, tak tady možnost post-hoc testování není. Nicméně musíme na tomto místě upozornit, že z podstaty věci je ANOVA explorativní analýza a s ohledem na nulové hypotézy jí nelze prokázat rozdíly, ale pouze jí můžeme nebo nemůžeme potvrdit neexistenci rozdílů. K interpretaci výsledků bychom měli primárně používat interakčních grafů a znalosti studovaného problému.

ANOVA pro porušení zásady nezávislosti měření (výběrů)

V pokusech můžeme mít nejčastěji dva typy plánovaných porušení nezávislosti měření. Prvním typem je porušení plynoucí z použití skupinového náhodného výběru a druhů, že opakujeme měření. Pro řešení prvního typu porušení nezávislosti výběrů je určena hierarchická ANOVA, pro druhý RMANOVA.

Hierarchická (Nested) ANOVA

Také v ní můžeme testovat více “faktorů”, ale o “faktorech” víme, že si nejsou rovnocenné, ale tvoří jistý hierarchický systém (na tabuli).

K porovnání dat z factorial a nested designu sběru dat.

Vulgárně řečeno, faktor nižší úrovně tvoří podmnožiny faktoru postaveného výše. Asi nejlepší na vysvětlení je příklad z učebnice (Lepš, 1996, s. 104) – autory zajímaly rozdíly délek korunních trubek u nějakého druhu hluchavky – styl, kterým vybrali květy není faktorový, ale je “nested” – navštíveny byly lokality a na lokalitách byly sebrány kytky a na nich byly měřeny vybrané květy. V podstatě můžeme říci, že se jedná o “bloky” (kytky) umístěné v “blocích” (lokality). Vysvětlovanou (závislou) proměnnou je samozřejmě délka korunní trubky. Nezávislou proměnnou je rostlina, na které jsme květy měřili a lokalita, na které jsme nasbírali ty kytky. Kytka je pak faktor s náhodným efektem. Lokalita může být fixed i random, podle situace pokusu – vzhledem k tomu, že autoři píší, že “porovnáváme lokality”, tak by měla být fixed.

Tady je asi zapotřebí upozornit na rozdíl mezi factorial a nested design – ten je primárně jasný z dat “faktorů”. Úplně znáhodnělé bloky, které jsme řešili při vysvětlování “fixed” versus “random”, jsou faktory, protože zásah typu 1 byl proveden v bloku 1, 2 i 3, zásah typu 2 byl proveden taktéž v bloku 1, 2 i 3. Naproti tomu kytka 1 (z předchozího odstavce) pochází jen z lokality 1, kytka 2 pochází jen z lokality 1, kytka 3 pochází jen z lokality 3, atd. Čili přinejmenším z kódování dat je jasné, jde-li o factorial nebo nested design (to uvádíme jen proto, že s tím jsou těžké problémy u zápočtu 🙂

Hierarchickou ANOVA v drtivé většině případů použijeme proto, že jsme naplánovali pokus nebo sběr dat na hierarchické úrovni (obvykle jde o skupinové náhodné výběry na jedné a více úrovních). Pro tento typ designu je pravidlem, že nás zajímá jen rozdíl skupin nejvyšší úrovně – tento faktor je pevný. Nižší “faktory” jsou zahnízděny v (nested in / nested under / nested within) skupinách (vyšší úrovně) – tvoří tedy podskupiny (subgroups). Konkrétní měřené vzorky jsou v nich vybrány náhodně a i tyto podskupiny jsou náhodným výběrem ze základního souboru podskupin – proto podskupiny (a případné další podpodskupiny) nastavujeme vždy jako náhodné faktory.
Přestože jsme na začátku uváděli nested design jako jeden ze způsobů designu experimentů, má tento design své uplatnění i v neexperimentálních výzkumných plánech. Nejčastěji se s ním v praxi setkáte, když budete dělat více měření na jednom objektu = na jedné lokalitě uděláte více měření (např. tam uděláte více vegetačních snímků nebo budete sledovat více transektů) nebo sledovanou proměnou změříte na jednom laboratorním zvířeti na několika místech jeho těla.

POZOR!!!!!

• V základním kurzu jsme pro řešení podobných (ne stejných!!!!) úloh používali One-way ANOVA – měli jsme tam ale jen jednu úroveň (= tu nejvyšší). Řešili jsme už jen konkrétní případy (= jejich rozdíly mezi skupinami nejvyšší úrovně) a neřešili jsme, že vzorky pochází ze specifických podskupin. Mohli jsme si to dovolit, protože jsme dat amístopsežně prohlásili z adata sebrané zce náhodně. Tento statistický postup vyhodnocení ale není v případech, kdy byly vzorky (konkrétní lokality, respondenti dotazníků, pokusní jedinci) vybírány skupinově, správný – je porušeno pravidlo nezávislosti jednotlivých měření (data jsou výsledkem pseudoreplikace). Musíme použít hierarchickou ANOVA s příslušným počtem úrovní skupin.
• Pokud nás zajímají i rozdíly v podskupinách a hlavně mezi nimi, pak je musíme nastavovat jako fixed a v těchto případech se už nepoužívá hierarchická ale faktorová ANOVA.

Hierarchickou ANOVA naleznete ve Statistice např. ve struktuře Statistics – Advanced models – General linear, kde je to položka Nested design ANOVA. V něm jsem schopen veškerá nastavení učinit.

• Příklad z přírodních věd: Jsme postaveni před otázku – Existuje souvislost mezi pokryvností Carex rostrata a množstvím minerálů rozpuštěných v podzemní vodě na jejím stanovišti? Pro studování této souvislosti byl zvolen Nested design. Základní vysvětlující proměnnou je minerální bohatost podzemní vody stanoviště prezentovaná dvěma stupni – minerálně bohatá versus minerálně chudá, v rámci těchto dvou typů stanovišť byly vybrány čtyři lokality a na nich provedeny dvoje měření pokryvnosti Carex rostrata. Řešení ve Statistica je na videu.

Práce s Nested ANOVA ve STATISTICA.

• Příklad ze sociálních věd: Zde je příklad jasný. V momentě, kdy mě zajímají rozdíly např. mezi lokalitami a data byla řešena sběrem dotazníky, kde bylo na každé lokalitě povícero tazatelů, tak by se neměla používat One-way ANOVA, ale hierarchická a jako podskupina by se mělo použít jednotlivých tazatelů, kteří jsou zahnízděni v lokalitě.

Na tomto místě se podívejme na další možnost ovládání testů v software Statistica – použití Analysis Wizard na příkladu nested design je na videu.

Ovládání Analysis Wizard ve STATISTICA.

ANOVA pro opakovaná měření (RMANOVA)

Testujeme vliv jednoho nebo více faktorů, které byly měřeny opakovaně (např. pH na lokalitě na jaře, v létě a na podzim nebo např. míra spokojenosti s ubytováním při první, při druhé a při třetí návštěvě daného hotelu). Podstatou tohoto opakování je, že lokalita byla změřena opakovaně na stejném místě nebo vzorek byl odebrán přesně ze stejného místa na zvířeti). V takových případech nemůžeme použít faktorovou ANOVA, pač měření pH na jaře a na podzim nejsou vzájemně nezávislé proměnné, stejně jako měření spokojenosti s prvním pobytem a třetím pobytem – musíme proto snižovat stupně volnosti. Už jsme i viděli, že jako závislé je považováno, když se v dotazníku ptáte respondenta na názor na větší množství např. produktů (s tím, že u každého produktu respondent rozhodoval na samostatné škále). Obecně je tento design označován jako “subject by trials design”. Ve své podstatě se jedná o factorial design, kde jeden faktor je tvořen vzájemně závislými měřeními.

STATISTICA má pro tato měření speciální nástroj volaný z karty ANOVA hlavní nabídky Statistics.

• Příklad z přírodních věd: Jako příklad si můžeme ukázat to, co jsme již řešili v základním kurzu. Otázkou je jestli se pH liší v typech vegetace podle druhové bohatosti, jestli se liší jednotlivá měření pH a jestli jsou tyto odlišnosti odlišné v typech vegetace podle druhové bohatosti? Řešení ve Statistica je na videu.

Výpočet RM ANOVA ve STATISTICA.

Pro všechny typy ANOVA platí, že v nastavení Sum of squares nastavujeme Type I nebo Type II, pokud máme vyvážené uspořádání, a Type III, pokud máme nevyvážené uspořádání, tedy různý počet měření v různých kombinacích proměnných, nebo některé kombinace měřeny nejsou – viz fractional factorial design – pro tyto případy jsou v nabídce i Type IV-VI.

Všimněte si, že u všech případů těchto komplikovanějších výzkumů, je zásadním už vlastní příprava měření – je třeba dopředu vědět, co proti čemu chci hodnotit, a podle toho nastavit systém sběru dat.

Návod na výpočet RM-ANOVA (jen faktor čas) pro MS Excel je na tomto externím odkazu.

Velikost účinku v lineárních modelech

Máme-li v modelu více nezávislých proměnných, které mají statistický vliv na nezávislou proměnnou, budeme postaveni před problém rozhodnout, jak důležité jsou. Už víme, že pro rozhodování o významu modelu jako celku používáme hodnotu adjusted R2, která nám říká z jakého podílu nám kombinace nezávislých proměnných vysvětluje variabilitu závislé proměnné. O důležitosti vlivu jednotlivých nezávislých proměnných na závislou proměnnou nám říká velikost účinku (effect size) – její mírou je v ANOVA modelech hodnota partial eta-squared.

Friedmanova ANOVA neboli Friedmanův test

Je neparametrickou obdobou testu ANOVA pro opakovaná měření (RMANOVA). Podobně jako Wilcoxonův test je výpočet založen na pořadí. Vzorec na výpočet testovacího kritéria je podobný Kruskal-Wallisovu testu. Vzorec včetně modelového výpočtu v MS Excel je na externím odkazu. Mnohonásobné porovnání se pak dělá na základě absolutní hodnoty rozdílu sum pořadí dvojice úrovní a jeho porovnání s tabelovanou hodnotou.
Friedmanův test se používá běžně v případech, kde není možné použít RMANOVA – teoreticky by se měla používat vždy, když máme ordinální data z dotaníků, která nejčastěji neoprávněně prohlašujeme za poměrová a navíc “normální”.
Bohužel Statistica nemá nástroj na “Two way” variantu tohoto testu, který by byl pravou náhradou RMANOVA (má ho ale např. Unistat). K dispozici máme jen jeho one-way variantu – tedy nejsme schopni jednoduše souběžně posoudit rozdíl v čase a mezi např. vegetačními typy, můžeme jen posoudit rozdíly v čase – video.

Friedmanův test ve STATISTICA.

Návod na výpočet Friedmanův test (jen faktor čas) pro MS Excel je na tomto externím odkazu.

ANCOVA

Pod tímto názvem se skrývá analýza kovariance. Tu použijeme v případě, že kromě kategoriálních skupin v jednofaktorové nebo vícefaktové ANOVA máme i poměrovou proměnnou, o které víme, že má vliv na velikost závislé proměnné. Vliv této proměnné chceme eliminovat, protože nás nezajímá, ale mi víme, že má vliv na sledovanou závislou proměnnou – použijeme ji v analýze jako tzv. kovariátu, jejíž vliv se nejprve od závislé proměnné “odečte” a následně se testuje rozdíl ve skupinách faktoru/ů. MS Excel v doplňcích analytických nástrojů ANCOVA nemá, nicméně pomocí regrese a ANOVA se k výsledku lze relativně jednoduše dobrat i v něm – návod je na externím odkazu. Ve STATISTICA je ANCOVA s sekci Statistics – Advanced models, a tam buď v General linear nebo, pokud chci nastavovat fixed versus random predictors, tak pak ve Variance components. Ani STATISTICA není schopna počítat s kovariátou nominálního charakteru, což je dost velké mínus pro ekologické experimenty – musí se použít CANOCO.

• Příklad z přírodních věd: Ústně jsme několikrát řešili na přednáškách v základním kurzu délky ocásků u tarbíků. Jenou z možností jak řešit problém rozdílnosti délky ocásků mezi pohlavími u tarbíka je použití modelu ANCOVA, kde vysvětlovanou proměnnou je délka ocásku, kategorickým prediktorem je pohlaví a kovariátou bude celková velikost jedince.

Pro práci v rozšiřujícím kurzu budeme používat software Dell Statistica. Je to komerční program zakoupený školou, který jsme vybrali proto, že je nainstalovaný na všech učebnách, je jednoduchý na ovládání a je schopen vyřešit většinu problémů, před kterými budete stát při vyhodnocování Vašich DP. Všechny další alternativy mají nějakou překážku v použití:

• SPSS je taktéž komerční program, který není školou koupen (především na neparametrické regrese je rozhodně lepší než Statistica)
• CANOCO, které je nejlepší pro mnoho zde zmíněných metod (především mnohorozměrnou statistiku), je komerčním programem, který není pro studenty fakulty pořízen
• B-VegAna, je sice freeware, ale běží na Javě a nemá schválen bezpečnostní certifikát, jeho instalace a pak především spouštění není ve škole možné (nicméně na domácí použití při řešení mnohorozměrných úloh ho důrazně doporučujeme)
• R je aktuálně nejpopulárnější free statistický software, není však všude nainstalováno (často chybí R-studio), jeho ovládání však není intuitivní a vyžaduje praxi, kterou není možné po studentech vyžadovat, jinak je to ale asi nejlepší řešení pro ty, co hodlají statistikovat data i po absolvování tohoto kurzu – na webu je návodů dost
• MS Excel, v něm jsme se naučili hodně, sami si můžete vyzkoušet věci další – je toho hodně – už jsme doporučovali RealStatistics a existuje noho komerčních “extenzí”, jako je např. Unistat
• ovládání většiny výše uvedených programů jsme vám zpřístupnili na zvláštních stránkách
• plus existuje noho komerčních programů řešících dílčí statistické úlohy

Stažení

Program máte k dispozici na \\archive.jcu.cz\Public Tuto lokalizaci musíte připojit jako síťovou jednotku. Budete to po Vás chtít autentizaci (je identická jako do STAGu). Program si stáhněte a nainstalujte – je tam více verzí – doporučuji stáhnout poslední a s tou pracovat. Návod je zde – POZOR!!!!!! je třeba opravdu připojovat \\archive.jcu.cz\Public a nikoliv \\archive.jcu.cz\public\Statistica\ jak je chybně uvedeno v návodu.

Program

Níže naleznete základní tutoriál pro práci s tímto software. Je to sice starší verze, nicméně většina věcí funguje stejně, jen na Windows 8 to vypadá trochu jinak než na Windows XP. Kromě importu dat je jako komplexní cvičná analýza uvedena jednocestná ANOVA plus korelace. Z toho by mělo být jasné základní ovládání programu, pokud něco jasného není tak doporučuji některá další videa, která má tenhle borec, je to sice v polštině, to by Vám ale jako slovanům nemělo vadit. Pokud se Vám to nezdá, tak původní majitel software StatSoft na to má svoje videa.

Při práci určitě používejte jejich učebnici – je vynikající.

Níže jsou videa, které jsem natočil pro bakalářky v roce 2009 ještě na starých verzích programu – zpracovávali jsme odpovědi z dotazníků, kde byly škály a nějaká segmentační kritéria:

• import dat do STATISTICA
• korelační matice ve STATISTICA a export do MS Excel
• ANOVA1
• ANOVA2
• úprava grafů ve STATISTICA
• zpracování výpočtů ANOVA ze STATISTICA v MS Excel do finální tabulky 1
• zpracování výpočtů ANOVA ze STATISTICA v MS Excel do finální tabulky 2
• ukončení práce

Pokud Vám nic z toho nepomohlo, tak základní manuál v češtině je tady.

POZOR!!! – funkčnost programu je obrovská a jeden požadavek lze uskutečnit průměrně 3 různými způsoby (to je alespoň náš odhad). Dále jsou uvedeny způsoby, které používáme my, a v žádném případě netvrdíme, že to jsou způsoby nejlepší nebo nejjednodušší.

Komě výše uvedeného ještě pro jistotu uvedeme základní práci, kterou jsme se naučili v základním kurzu zpracovat v ruce a v MS Excel. Vstupní data jsou v xls – v jednotlivých sloupcích jsou environmentální proměnné podzemní vody měřené na 21 místech v rašeliništní vegetací. Tyto proměnné byly měřeny obvykle 4x do roka (název sloupce se liší posledním číslem), kromě těchto environmentálních proměnných máme ve sloupcích ještě typ vegetace, jeho druhovou bohatost a typ druhové bohatosti). Pokud jste se software nikdy předtím nepracovali, tak začněte u těchto příkladů a pak se podívejte na další odkazy výše.

• import dat a rychlé získání histogramu a box plotu
• vytvoření grafu ze surových dat
• základní statistiky – parametrické
• základní statistiky – neparametrické

Pokud se ve výše uvedených videích hovoří o tom, že jsme to už viděli, tak příslušná videa naleznete obvykle v základním kurzu – v části, která je věnována konkrétnímu testu.

K zápočtu

Získání zápočtu je podmíněno ziskem v součtu alespoň 60 % bodů ze dvou zápočtových testů (platí pro PS; KS píše test jediný) a účastí na cvičení (povoleny jsou dvě absence; platí pro PS).

“Midterm exam”

Probíhá v polovině semestru – pokud nedojde k nějakému odpadnutí výuky, tak v 7. týdnu semestru, vždy po ukončení bloku věnovaného regresím. Předmětem tohoto testu je látka probíraná na 1.- 6. přednášce, tedy základní statistika v Statistica:

• chí-kvadrát testy,
• Fisherův exaktní test,
• t-testy,
• F-test,
• Mann-Whitney test,
• Wilcoxon test,
• jednofaktorová ANOVA,
• Kruskal-Wallis test,
• riedmanův test,
• parametrická a neparametrická korelace,
• jednoduchá a mnohonásobná lineární regrese,

a “advanced” typy ANOVA a regresních modelů:

• ANOVA hlavních efektů,
• faktorová ANOVA,
• heirarchická ANOVA,
• ANOVA pro opakovaná měření,
• ovládání nastavení pevných a náhodných efektů u výše uvedených typů ANOVA,
• regrese ze soudku GLM včetně nastavení metody výběru proměnných,
• regrese ze soudku GLZ včetně nastavení metody výběru proměnných.

Předmětem tohoto testu je ověření schopnosti řešit problémy kvantitativního zpracování dat v prostředí Statistica (po předchozí žádosti lze můžete použít i R, ale nemůžeme zaručit, že bude na té které učebně k dispozici).
Zadáno je vždy 6 úloh. Vybrané výsledky zapisujete do tištěného zápočtového testu. Na vypracování testu je k dispozici 75 minut.

Pravidla pro vypracování:

1. Pracujete výhradně s daty předanými pedagogem.
2. Při vypracovávání můžete používat Help STATISTICA.
3. Během vypracovávání zápočtu je zakázáno prohlížení jiných stránek než odkazů z Help STATISTICA.

 

Několik rad k úspěšnému zvládnutí testu:

• základní statistiky se ve většině případů v Dell Statistica nejmenují podle svého označení, proto je nutné vědět, kde je hledat
• výsledky software pro jednotlivé proměnné či kategorie reportuje různě podle nastavení konkrétní instalace a podle Vašeho zadání proměnných, čili se výstup může lišit od předepsaných polí v testu – je třeba si přečíst hlavičky v zadání testu ve výstupu, který vidíte na obrazovce
• u mnoha “advanced” typů ANOVA a regresí je třeba udělat po výpočtu ještě další operace, aby jste se dostali k výsledku, který je po Vás požadován

2. zápočtový test

Probíhá v zápočtovém týdnu. Předmětem také tohoto testu je ověření schopnosti řešit problémy kvantitativního zpracování dat v prostředí Statistica (po předchozí žádosti můžete použít R, ale pozor, nebudete si moct dohrát nástroje pro řešení úloh a my nemůžeme garantovat, že zrovna počítač, na kterém budete u zápočtu sedět, bude mít příslušné extenze nahrány).
Zadány jsou vždy 4 úlohy. Vybrané výsledky zapisujete do tištěného zápočtového testu. Na vypracování testu je k dispozici 60 minut.
2. zápočtový test je zaměřen na schopnost řešit složitější úkoly pomocí mnohorozměrných metod:

• hierarchická shluková analýza,
• nehierarchická shluková analýza metodou K-průměrů,
• PCA,
• FA,
• CA,
• MDS,
• CCorA,
• kanonická diskriminační analýza,
• klasifikační diskriminační analýza.

Pravidla pro vypracování:

1. Pracujete výhradně s daty předanými pedagogem.
2. Při vypracovávání můžete používat Help STATISTICA.
3. Během vypracovávání zápočtu je zakázáno prohlížení jiných stránek než odkazů z Help STATISTICA.

Pokud jste z důvodu absence neabsolvovali “midterm exam”, pak jej absolvujete společně s 2. zápočtovým testem v zápočtovém týdnu.

Pokud v součtu “midterm exam” a 2. zápočtového testu nezískáte minimálně 60 %, musíte absolvovat oba testy společně v opravném termínu – opravné termíny máte dva.

Jelikož se ukázalo jako nemožné provést “midterm exam” pro kombinované studium, bude kombinované studium psát oba testy společně v jednom termínu, na kterém se dohodneme na první konzultaci!!!!!!!!!

Ke zkoušce

Zkouška je teoretická a probíhá písemnou formou testu. Test se skládá ze 14 otázek na teorii ohledně přípravy výzkumu, zpracování dat různých přístupů analýzy variance (všechny probrané typy ANOVA), regresních modelů (linear, normal, binomial, multinomial, ordinal), shlukových analýz (K-means, hiararchická) a ordinačních analýz (PCA, RDA, DCA/CA, CCA, CCorA) včetně MDS/NMDS a diskriminační analýzy. Typickými otázkami jsou otázky na to, kdy jakou analýzu použít, v čem se podobné analýzy liší, jaké mají předpoklady, co mohu vyčíst z ordinačních diagramů. 10 otázek je testových – za každou správnou odpověď (čtyři možnosti na výběr, právě jedna z nich správná) získáte bod – a 4 otázky jsou textové – za každou správnou odpověď získáte bod. K absolvování zkoušky je třeba 8 bodů. Čas na vypracování je 25 minut.

Známkování:

• 8 bodů 3
• 9 bodů 2-
• 10 a 11 bodů 2
• 12 bodů 1-
• 13 a 14 bodů 1

 

Obecně se jedná o statistické ukazatele síly vazby/vlivu proměnné.

Vysvětlení variability jedné proměnné proměnnou jinou

Ty známe z předchozího:

• korelační koeficient
• koeficient determinance

Rozdíly mezi průměry dvou veličin

• Cohenovo d

Posouzení stejnosti nominálních proměnných

• odds ratio

Posouzení velikosti vlivu jednotlivých proměnných v lineárních modelech

• partial eta-squared

vypočítá se jako SSeffect / (SSeffect + SSerror), kde SSeffect je SS příslušní proměnné SSerror je chyba SS modelu

pokud je více proměnných signifikantních díváme se na partial eta-squared, kde vidíme jaký je význam vlivu jednotlivých proměnných v modelu, je to jako v korelaci – signifikave nám říká, že vazba je, ale partiall eta-squared nám říká jak je veliká

Regrese se naučíme v poslední 11. lekci R pro základní kurz.

Jednoduchá lineární regrese

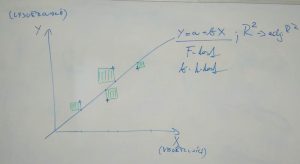
Pokud jsme schopni určit, která proměnná je závislá (značíme ji obvykle Y nebo Lhs od “left hand side”) na které nezávislé proměnné (značíme ji obvykle X nebo Rhs od “right hand side”), pak hovoříme o regresi (máme-li jen dvě takové proměnné, pak o regresi Y na X) – předchozí kovariance a korelace byly o vzájemných vazbách, ne závislosti. V regresi však nemusí jít nutně o závislost, ale často jde o snahu vysvětlit variabilitou proměnné X variabilitu Y při vědomí toho, že Y nemusí být přímo explicitně na X kauzálně závislá. Často tedy regresi používáme k vysvětlení variability jedné proměnné nějakou jinou proměnnou jinou o níž víme, že patří do skupiny proměnných, na níž první proměnná závisí. Nejjednodušším případem regrese je hledání lineární závislosti jedné vysvětlované proměnné na jedné vysvětlující proměnné.

Princip uvažování je podobný jako u ANOVA (jedná se o metodu, která patří do stejné skupiny metod označovaných jako obecné lineární modely). K nejdůležitějším bodům patří:

• data musí mít poměrový charakter s normálním rozdělením

• podstatou je získání takové lineární funkce, že pro každé měřené X je součet čtverců rozdílů (reziduí) mezi měřeným Y a Y, získaným z této funkce, minimální
• výsledkem regrese je tak především funkce přímky, která prochází mrakem bodů XY grafu, kterou lze zapsat jako Y= a +bX, “a” je pak průsečík přímky s osou Y (= intercept) a “b” je směrnice udávající sklon přímky
• statistická významnost modelu se testuje pomocí F testu, který je analogií F-testu v ANOVA, jde tedy o test průměrných čtverců regrese a reziduí (F = MSreg / MSe), kde se průměrné čtverce (stejně jako v ANOVA) počítají jako podíl součtu příslušných čtverců rozdílů od průměru (SSreg = SUMA (reziduum Y – průměr Y)2; (SSe = SUMA (Y – reziduum Y)2) a počtů stupňů volnosti (dfreg = 1; dfe = n-2)
• dále se testuje rozdílnost parametru “b” od nuly, protože, kdyby byl roven nule, pak Y nezávisí na X (rovnice by pak měla vzorec Y = a) – používá se t-testu, kde v čitateli je hodnota “b” a ve jmenovateli střední chyba b
• významným ukazatelem je pak hodnota koeficientu determinance (R2), který udává procento vysvětlené variability vysvětlované proměnné hodnotami vysvětlující proměnné a počítá se jako SSreg / (SSreg + SSe)

• Příklad z přírodních věd 1: Z videí u korelací můžeme jako příklad vzít snahu o vysvětlení druhové bohatosti hodnotami pH podzemní vody.

• Příklad z přírodních věd 2: Existuje závislost biomasy samců na velikosti samice ostrorepa, která tyto samce nese při rozmnožování? Použijte soubor korelace.xlsx a proměnné samci_biomasa a samice_hmotnost.
• Příklad ze sociálních věd: Jaká je závislost ochoty návštěvníka zámku doporučit jeho návštěvu známým (měřené na 7-stupňové škále) na jeho spokojenosti s návštěvou (měřené na 7-stupňové škále).

Videoprezentace

Výpočet v MS Excel je jednoduchý a je nahrán na videu.

Mnohonásobná lineární regrese

Obvykle nezávislých proměnných měříme více a hledáme takovou proměnnou nebo takovou kombinaci proměnných, která statisticky významně vysvětlí závislou proměnnou. Do modelu vstupuje vždy větší počet vysvětlujících proměnných než jedna – identifikujeme tak větší počet koeficientů b (ke každé nezávislé proměnné). Odlišnost koeficientu b od nuly se testuje jako v jednoduché regresi t-testem. Stejně tak celkový model se testuje F-testem. Pro odhad vysvětlené variability se na místo koeficientu determinance (R2) používá upraveného koeficientu determinance – adjusted R2 (uvádí např Lepš, 1996, Vz. 14-7, kde m je počet nezávislých proměnných). Je třeba si uvědomit, že výsledek analýzy se bude lišit podle kombinace použitých vstupních nezávislých proměnných.

Výsledek mnohonásobné regrese je vždy třeba posoudit regresní diagnostikou v níž se posuzují data, model a metoda odhadu. Cílem je získat co nejjednodušší a přitom co nejpřesnější a statisticky významný model. Regresi tak opakujeme několikrát, vždy po úpravách složek diagnostiky – především se jedná o úpravy v datech (odstraňování odlehlých hodnot měření) a zařazování proměnných (= jejich výběr). K tomu jsou určeny statistické programy. S ohledem na výpočtové procedury je nutné dodržet pravidla pro mnohonásobnou lineární regresi – zejména normalitu dat jako u jednoduché lineární regrese a dále zabránění multikolinearitě (tedy vzájemné závislosti dvou a více nezávislých proměnných) a heteroskedascititě (tedy závislosti variance na hodnotě proměnné – provádí se Durbin-Watson testem, což je test autokorelace reziduálů, návod je kupříkladu na externím odkazu). Outliery lze nejjednodušeji identifikovat pomocí reziduálů, stejně tak i heteroskedasticitu. U odstraňování outlierů dávejte pozor – je vhodné se podívat, co za měření přesně odstraňuji a zvážit proč nesedí na model (jejich odstraňování zpochybňuje sběr dat). Multikolinearita je jedním s nejčastějších problémů a také asi nejtěžším problémem mnohonásobných regresí. Pokud multikolinearita existuje, pak obvykle regresní model vykazuje statisticky významný F-test, vyšší hodnoty koeficientu determinance, ale hodnoty b se t-testem neliší průkazně od nuly. Taktéž minimální změny v datech vedou ke zcela odlišným modelům, ty jsou tedy vysoce nespolehlivé. Dalším identifikátorem, že v modelu hraje roli multikolinearita, jsou vysoké hodnoty střední chyby odhadu. Obecně platí, že multikolinearitu nelze testovat, jen měřit. Kromě výše uvedených indicií se používá jednoduchých a vícenásobných korelačních koeficientů nezávislých proměnných. Hodnoty velmi blízké +1 a -1 mohou znamenat kolinearitu, ale nemusejí, proto by se vždy měl použít některý z dalších nástrojů měření – je jich velké množství k nejjednodušším patří Scottovo testační kritérium M

M1(2, . . .m) = (F/(1/m*SUMA(j=1)m (tj2)) – 1) / (F/(1/m*SUMA(j=1)m (tj2)) + 1)

kde F = hodna F statistiky regrese, t = hodnota t-statistiky všech regresních koeficientů s výjimkou interceptu (a), j = číslo pořadí nezávislého faktoru a m = počet nezávislých faktorů. Pak hodnota větší než 0,8 indikuje silnou multikolinearitu, od 0,33 do 0,8 mírnou kolinearitu

Dále se používá Variance Inflation Factor – zapotřebí je připravit inverzní korelační matici a hodnoty na diagonále (kde byly původně jedničky) vyšší než 10 indikují, že daná proměnná je lineární kombinací jiných proměnných. Odstranit ji lze vypuštěním “nadbytečných” proměnných – rozhodování je obtížné, navíc víme-li, že mezi nezávislými a závislou proměnnou existuje větší počet “kauzálních ” vazeb. Vypuštěním proměnné často dostaneme model, který nebude ve finále správný. Řešit to můžeme použitím jiné metody než je metoda nejmenších čtverců.

Vzhledem k tomu, že cílem je obvykle sestavit co nejjednodušší model, lze některé měřené proměnné z modelu vyřadit – buď ručně porovnáním dílčích regresních modelů nebo automaticky. Já používám proceduru krokového dopředného výběru, kdy jsou do modelu zařazovány postupně proměnné, které vysvětlují největší podíl variability nevysvětlené do modelu už zařazenými vysvětlujícími proměnnými (Forward Stepwise Selection).

Pro používání mnohonásobné lineární regrese je nutné nastudovat větší množství literatury – je to poměrně komplikovaná záležitost – externí odkazy např. tady, tady, tady, nebo tady.

Pokud nejsou splněny předpoklady pro použití lineární regrese, lze data nejprve transformovat nebo použít nelineární regrese, to vše ale je už za hranicemi základní statistiky a je mu věnován prostor v rozšiřující statistice.

• Příklad z přírodních věd: Identifikace závislosti pokryvnosti Drosera rotundifolia na chemických vlastnostech podzemní vody – měřeny byly: amoniakální dusík, dusičnanový dusík, celkový fosfor, vápník, železo, a sírany. Kvůli multikolinearitě byly některé měřené vlastnosti z analýzy vypuštěny.

Videoprezentace

Mnohonásobnou lineární regresi lze provádět přes Analytické nástroje i v MS Excel – je to stejný modul, jako v případě jednoduché lineární regrese, jen zadáte větší počet nezávislých proměnných. Ve výsledcích se lze dostat i v něm k tabulkám reziduí, grafům a parciálním regresním koeficientům. Základní postup zadání je na videu. Pokud byste potřebovali více informací, tak ty jsou kupříkladu volně dostupné na externím odkazu.

S ohledem na další možnosti nastavení budeme v rozšiřujícím studiu k řešení mnohonásobné lineární regrese používat software Statistica. Výpočet příkladu ve Statistica na videu.

Hodnoty b* jsou standardizovanými hodnotami parciálních regresních koeficientů a udávají tak “relativní význam” proměnné v rámci celého modelu, pro konstrukci rovnice musím použít koeficienty b (bez hvězdičky).

Řešení předchozího příkladu ve Statistice s využitím Forward Stepwise Selection je na videu.

Už v předchozích částech jsme řešili problematiku závislosti či nezávislosti výběrů. Řekli jsme si, že tu jsme schopni řídit designem sběru dat či výběrem objektů pro experiment. Kromě tohoto problému patří k základním statistickým metodám ještě řešení problému vzájemné souvislosti měřených náhodných veličin. Na tomto místě se podíváme na vyjádření vzájemné souvislosti, dále i na závislosti náhodných veličin, které jsme na objektech změřili.

Kovarianci a korelaci se naučíme v 10. lekci R.

Videoprezentace

---

Kovariance

Je základním ukazatelem vzájemné souvislosti (založené na variabilitě) dvou náhodných veličin. Jde v podstatě o hodnotu společného rozptylu a z výpočtu rozptylu také vychází. V MS Excel je na její výpočet funkce COVARIANCE.S. v R je to jednodušší – příkaz zní cov(). Kovarianci značíme obvykle cov(XY) nebo s(XY) a pro spojitou veličinu ji lze vypočítat jako:

cov(XY) = SUMA(i = 1 až n) ((Xi – průměr X)*(Yi – průměr Y)) / (n-1)

• pokud je cov(XY) větší než 0, pak je souvislost mezi veličinami X a Y pozitivní, čím je větší X tím je větší Y a naopak
• pokud je cov(XY) menší než 0, pak je souvislost mezi veličinami X a Y negativní, čím je větší X tím je menší Y a naopak
• platí, že nezávislé veličiny mají cov(XY) rovnu nule, ale bohužel neplatí, že by cov(XY) rovnou nule znamenalo, že X a Y jsou nezávislé
• kovariance nám neříká také nic o síle vazby – je vyjádřena v jednotkách X a Y

V praktické statistice základní úrovně se hlavně z důvodu výše uvedených nevýhod moc nepoužívá (místo ní se používá korelace – viz dále). Svůj velký význam má kovariance v mnohorozměrných analýzách, kde je matice kovariancí velkého množství proměnných vstupem do vlastních analýz. POZOR – na diagonále kovariační matice je hodnota rozptylu dané proměnné.

• Příklad z přírodních věd 1: Existuje souvislost v koncentracích vápenatých a hořečnatých iontů v podzemní vodě sytící slatiniště? Na větším počtu lokalit jsme odebrali po jednom vzorku vody, dám udělat rozbor množství iontů v každém vzorku a zajímá mě, jestli je mezi oběma hodnotami zjištěnými na jednotlivých lokalitách nějaká vazba. Použijte soubor data1.xlsx a proměnné Ca1 a Mg1.
• Příklad z přírodních věd 2: Existuje souvislost mezi velikostí samice ostrorepa a biomasou samců, které nese při rozmnožování? Použijte soubor korelace.xlsx a proměnné samci_biomasa a samice_hmotnost.
• Příklad ze sociálních věd: Existuje souvislost hodnocení spokojenosti s návštěvou zámku (měřené na 7-stupňové škále) a ochotou jeho návštěvu doporučit známým (měřené na 7-stupňové škále)? V dotazníku se ptám návštěvníků na obě proměnné a potom porovnávám odpovědi v dotaznících.

Videoprezentace

---

Korelace

Párová korelace

Korelací rozumíme taktéž statistickou souvislost dvou obvykle kvantitativních proměnných. Na rozdíl od kovariance je však vyjádřením míry této souvislosti. Míra (= síla) souvislosti je dána korelačním koeficientem. Základním rozdílem od kovariance je jeho bezrozměrnost (hodnota je nezávislá na jednotkách obou veličin) a normalizované vyjádření = může nabývat hodnot v intervalu od -1 do 1; kde 1 znamená 100% pozitivní souvislost, -1 znamená 100% negativní souvislost a 0 znamená absolutní nezávislost.

Korelační koeficient používáme často při prvním náhledu na strukturu sebraných dat. Nejčastěji se používá Pearsonův korelační koeficient, jehož vzorec je na tabuli. Dobré výsledky však dává jen při splnění předpokladu normality rozdělení porovnávaných proměnných.

V MS Excel má funkci CORREL,

V R zní příkaz pro korelaci cor().

Také pro korelační koeficient se testuje jeho významnost. Jejím problémem ale je, že ta je funkcí počtu měření – s narůstajícím počtem měření tedy stačí pro “prokázání” statistické významnosti koeficient s hodnotou stále bližší nule. Obecně platí, že “prokázání” souvislosti závisí především na řešeném problému – v případě porovnání měření jedné veličiny dvěma přístroji nebudeme s korelací 0,95 spokojeni, ale v případě zjištění korelace 0,35 mezi výdaji turisty na dovolené a mírou jeho zájmu o určitý produkt, budeme tuto hodnotu považovat za prokázání korelace. Statistická významnost bude v obou případech hrát v praxi podružnou roli, nicméně pro BP a DP byste se měli primárně vyjadřovat ke koeficientům, které jsou statisticky významné – pokud budete mít dostatečný počet měření a mezi proměnnými souvislost opravdu existuje, pak by s prokázáním statistické významnosti koeficientu neměl být problém.

Často ovšem neměřím jen dvě proměnné, ale větší množství vztahující se k řešenému problému – pro každou dvojici počítám korelační koeficient a výsledkem je korelační matice, tedy symetrická matice, kde na diagonále jsou samé jedničky.

Výpočet korelační matice Pearsonových korelačních koeficientů je v MS Excel jednoduchý a je na videu. Ovládání ve Statistica je na videu.

• Příklady: jsou stejné jako u kovariance

Pro data, která nesplňují podmínku normality dat, se běžně používá vícero neparametrických korelačních koeficientů – nejčastěji používaným je Spearmanův koeficient pořadové korelace, jehož vzorec je na tabuli, popřípadě Kendall-Tau korelační koeficient.

Návod na výpočet v MS Excel je na externím videu. Lze jej použít pro poměrová data, která nesplňují podmínku normality, pro ordinální data (pro která jsou primárně tyto koeficienty určeny), i data nominální – u nich je však třeba dát si pozor na kódování (bezpodmínečně musíte použít bivariátní kódování = jedna proměnná bude mít tolik sloupců, kolik je kategorií této proměnné – řešili jsme to v typech dat).

• Základní příklady: jsou stejné jako u kovariance
• Další příklad z přírodních věd: Chci-li korelovat hodnotu pH s geologickým substrátem, musím mít geologický substrát zadán jako bivariátní proměnnou a ne jako vícekategoriální nominální proměnnou. Korelovat mohu nikoliv geologický substrát, ale zvlášť žulu, rulu, svor, atd.
• Další příklad ze sociálních věd: Chci-li korelovat hodnotu míry spokojenosti s ubytováním v hotelu s věkovou kategorií, musím mít věkové kategorie zadány jako bivariátní proměnnou a ne jako vícekategoriální nominální proměnnou. Korelovat mohu nikoliv věkové kategorie, ale zvlášť věk 18-25, 25-35, 35-45, atd.

Pro korelační koeficienty lze testovat statistickou významnost, která se odvíjí od počtu měření – čím mám větší počet měření, tím mi k prokázání významnosti stačí nižší absolutní hodnota korelačního koeficientu. POZOR!!!! – statistická významnost koeficientu však není statistickým důkazem kauzality, jde pouze o identifikátor existence nebo neexistence “nějaké” vazby mezi náhodnými veličinami. Také platí, že tato vazba nemusí být přímá, ale je zprostředkovaná nějakou další proměnnou.

Vzhledem k tomu, že obvykle měřené proměnné jsou vzájemně “prokorelované”, pak mě často zajímají čisté závislosti a používám parciálních korelací, nebo celkový vliv měřených proměnných na jednu proměnnou, pak používáme mnohonásobnou korelaci.

Parciální korelace

Závislost dvou proměnných může být ovlivněna závislostí obou těchto proměnných a proměnnou třetí (čtvrtou, pátou, atd., podle toho, kolik jsme jich naměřili). Pokud máme větší počet proměnných můžeme se pokusit zjistit závislost dvou proměnných bez vlivu ostatních měřených proměnných. K tomu se používá parciálních korelačních koeficientů. Ty jsou různých řádů – počet řádů je dán počtem vyloučených proměnných (pokud vlivu dvou veličin vyloučím vliv dalších tří měřených, pak se jedná o parciální korelaci třetího řádu). Ono “vyloučení” znamená, že “vyloučené” proměnné zůstávají neměnné = konstantní.

Parciální koeficienty se počítají různě, pro MS Excel lze výhodně použít vzorec, který uvádí Meloun:

R1i(2,3, . . .m) = ((-1)i*DETERMINANT(R1,i)) / (ODMOCNINA(DETERMINANT(R1,1)*DETERMINANT(Ri,i))

kde R je korelační matice všech měřených proměnných, kde v prvním řádku a sloupci je proměnná pro niž chci počítat parciální korelační koeficient a na i-tém místě je proměnná s níž chci proměnnou v prvním řádku a sloupci korelovat; matice (R1,i) vzniká z korelační matice R odstraněním prvního řádku a sloupce v němž se nachází druhá proměnná pro parciální korelaci; matice (R1,1) vzniká z korelační matice R odstraněním prvního řádku a prvního sloupce; matice (Ri,i) vzniká z korelační matice R odstraněním řádku a sloupce v nichž se nachází druhá proměnná pro parciální korelaci. Důrazně doporučujeme (s ohledem na minimalizaci generování chyb) ve výpočtu, dávat druhou proměnnou pro výpočet parciálního korelačního koeficientu na druhé místo.

POZOR!!!!! – z výpočtu je jasné, že “čistá” korelace po odfiltrování vlivu jedné nebo více proměnných je závislá na tom, co za proměnné mám naměřeno. S ohledem na tuto skutečnost je třeba výsledky interpretovat.

Příklad výpočtu v MS Excel je na videu.

Mnohonásobná korelace

Mnohonásobný (nebo vícenásobný) korelační koeficient určuje míru závislosti mnou zvolené měřené proměnné a nejlepší kombinace všech dalších měřených proměnných. Taktéž jej uvádí Meloun:

R1(2, . . .m) = ODMOCNINA(-1*(DETERMINANT(R) / DETERMINANT(R1,1))

kde R je opět korelační matice všech měřených proměnných, kde v prvním řádku a sloupci je proměnná pro niž chci počítat mnohonásobný korelační koeficient; matice (R1,1) vzniká z korelační matice R odstraněním prvního řádku a prvního sloupce.

Pokud výsledný korelační koeficient umocníte na druhou a vynásobíte stem, tak získáte procentickou hodnotu, ze které variabilita všech dalších proměnných vysvětluje variabilitu zvolené proměnné (té, co je na prvním řádku a v prvním sloupci). R nic základního v počtu R nemá a mi se na něj podíváme příště u regresí, kde upravené R² je jedním z hlavních výsledků.

Výsledky mnohonásobné korelace nás už totiž posunuly k jinému typu závislosti, od typu “A” souvisí “B” k typu “A” je závislé na “B”, tedy k regresi.

Příklad výpočtu v MS Excel je na videu.

Videoprezentace

Máme-li více výběrů než dva, nemůžeme řetězit dvouvýběrové t-testy ani jejich neparametrické varianty, ale musíme použít speciální metody výpočtu označované obecně jako ANOVA a její neparametrické obdoby. Dostáváme se na půdu lineárních modelů a jejich neparametrických rozšíření a tedy půdu již poměrně komplikovanou 🙂

Všechny na tomto postu uvedené testy naleznete v 9. Lekci R.

Rozhodování o metodě

Mám data z více výběrů, které jsou nezávislé, ale mohou být závislé.

1a Data jsou poměrová a splňují podmínku homogenity variancí a pocházejí ze souborů s normálním rozdělením . . .  2 ANOVA

1b Data výše uvedenou podmínku nesplňují nebo nejsou poměrová . . . 3 neparametrické testy

2a  Všechny výběry nezávislé . . .  klasická ANOVA

ANOVA	vyvážený design	nevyvážený design
jednofaktorová	Typ I	Typ III
hlavní efekt	Typ I	Typ II
vícefaktorová	Typ I	Typ III
nested	Typ I	Typ III

2b Alespoň jeden výběr závislý . . . RMANOVA

Klasická ANOVA i RMANOVA mohou pracovat s faktory s pevnými efekty i náhodnými efekty.

3a Všechny výběry nezávislé . . . Kruskal-Wallis test

3b Alespoň jeden výběr závislý . . . Friedmanův test

Videoprezentace

---

ANOVA jednoduchého třídění (One-way ANOVA)

Tento test je základní a používáme ho, chceme-li posoudit hypotézu o rovnosti průměrných hodnot více než dvou výběrů. Předpoklady použití ANOVA jednoduchého třídění jsou:

• nezávislost porovnávaných výběrů,
• homogenita variancí výběrů, testujeme Leveneovým testem, jehož vzorec najdete např. v externím odkazu,
• výběry pocházejí ze základních souborů s normálním rozdělením,
• všechny výběry by měly mít stejný počet n, nebo alespoň srovnatelný.

Užití si můžeme demonstrovat na následujících příkladech:

• Příklad z přírodních věd 1: v šetřeném území se vyskytuje větší počet typů vegetace vázané na mokřady – typ vegetace zjistím analýzou druhového složení (např. podle Chytrý et al., 2012 nebo s využitím nějaké sofistikované statistické metody) a zajímá mě, jestli se dané typy vyskytují na shodných stanovištních podmínkách, takže změřím např. pH, konduktivitu a výšku hladiny podzemní vody. Pro každou z těchto tří měřených proměnných pak mohu zjišťovat jestli se průměrné hodnoty měřené v jednotlivých typech vegetace liší nebo nikoliv.
• Příklad z přírodních věd 2: Pěstujeme rostlinný druh ve třech typech substrátu. Liší se výška rostliny po roce pěstování? Všechny ostatní faktory byly designem eliminovány. Použijte soubor vice_vyberu.xlsx a proměnné substrat a vyska).
• Příklad ze společenských věd: zajímá mě odpověď na otázku: “Liší se spokojenost s návštěvou zámku podle vztahu návštěvníka k historii?” Musím provést výběrové šetření, kde se budu návštěvníků ptát na jejich vztah k historii (5 kategorií – historie je pro mě velmi zajímavá, historie je pro mě zajímavá, historie je pro mě nezajímavá, historie je pro mě zcela nezajímavá, nedokážu se rozhodnout) a jejich míru spokojenosti, kterou budu měřit na 9-ti členné škále). Mezi pěti kategoriemi vztahu k historii pak budu hledat rozdíly v průměrných hodnotách odpovědí na spokojenost.

Analýza rozptylu se technicky provádí ve dvou krocích:

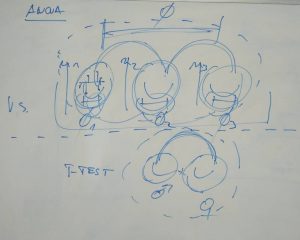
1. Nejprve testuji poměr variance uvnitř definovaných skupin (typ vegetace nebo typ návštěvníka hradu podle vztahu k historii) a rozptylu celkového souboru získaných dat. Jde tedy v podstatě o F-test. Rozptyly zde jsou označovány jako MS (F= MS(celek)/suma MS(ve skupinách)). Rozptyly jsou určeny jako podíly součtu čtverců odchylek od průměrů a počtu stupňů volnosti. Přehled informací k prvnímu kroku je na tabuli.

2. Pokud zjistím, že hodnota F je vyšší než kritická hodnota pro daný počet stupňů volnosti (= p je menší než stanovená hladina významnosti), pak vím, že v mém souboru dat existují rozdíly mezi skupinami, musím se proto dále ptát: “Jaké skupiny vegetace nebo jaké skupiny návštěvníků hradu se od sebe liší?” Následuje tedy fáze mnohonásobného porovnávání, kdy se testuje rozdílnost skupin pomocí tzv. post-hoc testů. K nim je obvykle nutné znát dosažené hodnoty rozptylů, stupně volnosti a počet měření pro jednotlivé testované skupiny. Těchto testů je mnoho, obecně se používá Tukeyho post-hoc test, jehož výpočet je odvozen od t-testu a má variantu pro vyvážený i nevyvážený design. Kritické hodnoty pro jeho q statistiku lze nalézt na externím odkazu (R počítá přímo i hodnotu p). Přehled informací ke druhému kroku je na tabuli.

Analogií Tukeyho post-hoc testu je Dunnettův post-hoc test, kterým porovnáváme nikoliv všechny skupiny mezi sebou, ale všechny skupiny s kontrolní skupinou. Použije jej tedy, pokud provádíme experiment, kde máme jednu bezzásahovou skupinu (= kontrolu).

Další testům “klasické” ANOVA se budeme věnovat podrobněji v navazujícím kurzu.

Postup řešení výpočtu jednofaktorové ANOVA v MS Excel je na videu.Postup výpočtu Tukeyho post-hoc testu v MS Excel je na videu.Dunnettův post-hoc test se dá vypočítat i v MS Excel, jako je na externím videu. Ve STATISTICA jej najdete v dialogovém okně ANOVA Results na kartě post-hoc úplně dole (pokud znáte směr, tak můžete použít jednostranného testu; nezapomeňte nastavit, která úroveň je kontrola).

Videoprezentace

Postup řešení výpočtu jednofaktorové ANOVA v MS Excel je na videu. Postup výpočtu Tukeyho post-hoc testu v MS Excel je na videu. Dunnettův post-hoc test se dá vypočítat i v MS Excel, jako je na externím videu. Ve STATISTICA jej najdete v dialogovém okně ANOVA Results na kartě post-hoc úplně dole (pokud znáte směr, tak můžete použít jednostranného testu; nezapomeňte nastavit, která úroveň je kontrola).

---

RMANOVA = ANOVA pro opakovaná měření

Je-li One-way ANOVA analogií dvouvýběrového t-testu pro více výběrů, pak RMANOVA je obdobou pro párový t-test, kde máme více opakování než jedno. Tento test použijete v případech, když výběry nejsou vzájemně nezávislé – typicky, když měříte jeden objekt více než dvakrát. Výpočet v R se odvíjí od výpočtu vícefaktoriální ANOVA (viz navazující kurz).

• Příklad z přírodních věd 1: Odebíráte vzorek tkáně z jednoho zvířete na čtyřech místech a ptáte se, jestli záleží na tom, ze kterého místa odběr provádíte.
• Příklad z přírodních věd 2: Měříte fyzikálně chemické vlastnosti substrátu na jaře, v létě a na podzim a ptáte se, jestli se odběry v těchto třech termínech liší.

Videoprezentace

Použití MS Excel pro tento výpočet máte na externím zdroji.

---

Kruskal-Wallis test neboli Kruskal-Wallis ANOVA

Pokud jsou předpoklady pro použití ANOVA výrazně porušeny, používáme Kruskal-Wallis test. Ten je neparametrickou obdobou testu (jedno)faktorové ANOVA. Podobně jako Mann-Whitney test, je i výpočet Kruskal-Wallis testu založen na pořadí. Používáme ho v případě, kdy je zjevně porušena normalita v rozložení měřených dat – což se v terénu obvykle stává často – nebo máme ordinální data. Kruskal-Wallis test se běžně používá a v mnoha případech je jeho použití správnější než ANOVA jednoduchého třídění. Vše podstatné je na tabuli.

Tabulka kritických hodnot je na např. na externím odkazu 1 nebo externím odkazu 2. Také u Kruskal-Wallis testu je v případě prokázání rozdílů mezi skupinami nutné provést test shody dvojic měřených úrovní. Existuje mnoho takových testů, ale nejčastěji se provádí Mann-Whitney testem pro jednotlivé páry s upraveným p podle Bonferoniho korekce – blíže na externím odkazu.

• Příklad z přírodních věd 1: Liší se pH na stanovištích třech typů vegetace? Použijte stejný soubor a data, jako u videa k jednocestné ANOVA.

Videoprezentace

STATISTICA má tento test schován v nabídce karty “Nonparametrics” pod označením “Comparing multiple indep. samples (groups)”.

---

Friedmanův test

Je-li Kruskal-Wallis test analogií Mann-Whitney testu pro více výběrů, pak Friedmanův test je obdobou pro Wilcoxonův test, kde máme více opakování než jedno. Tento test použijete v případech, když výběry nejsou vzájemně nezávislé – typicky, když měříte jeden objekt více než dvakrát a zároveň máte porušeny pravidla pro použití RMANOVA (především často nemáte “normální” data).

Příklady jsou stejné jako v případě RMANOVA, jen data nesplňují podmínky použití RMANOVA.

Videoprezentace

Použití MS Excel pro tento výpočet máte na externím zdroji.

Neparametrické metody jsou určeny primárně pro testování statistických hypotéz týkajících se nominálních a ordinálních dat – jsou na nich definovány. V případě dat nominálních vyhodnocujeme četnosti – jen ty mají kvantitativní charakter, jinak vlastní nominální data mají informaci kvalitativní (pohlaví, barva, typ čehokoliv). Testování hypotéz u ordinálních dat se děje na základě pořadí zjištěných hodnot – v testech se nepracuje se přímo s měřenými hodnotami, ale s jejich pořadími.

Využít tyto metody lze i pro data vyšší úrovně. V případě, že tato data nesplňují některou z podmínek testů určených pro tyto data, a my je musíme testovat, pak nemáme na výběr, a použijeme neparametrických metod. Nicméně, pokud je to možné, měli bychom na poměrová data použít metod parametrických.

Videoprezentace

---

NOMINÁLNÍ DATA (7. lekce R)

První skupinou metod jsou metody definované na nominálních datech a určeny tak jsou především pro testování hypotéz spojených s četnostmi výskytu.

Videoprezentace

---

Chí-kvadrát testy

Hodnoty důležité pro výpočet chí-kvadrát testu jsou obvykle zjistitelné z kontingenční tabulky našich dat. Vzorce pro výpočet jsou uvedeny u jednotlivých typech testů.

MS Excel je schopen jej vypočítat pomocí funkce CHITEST (nové verze používají funkci CHISQ.TEST), jen si budete muset sami napsat nebo vypočítat očekávané hodnoty (navíc MS Excel vrací jen hodnotu p a nikoliv chí-kvadrátu a d.f., přestože návod tvrdí opak).

Nejčastěji používáme chí-kvadrát test ve dvou typech případů:

Testuji rozložení mé jedné proměnné oproti předpokládanému (teoretickému) rozložení této proměnné = jednovýběrový chí-kvadrát test dobré shody

Základní informační shrnutí je na tabuli.

• Příklad z přírodních věd 1: sleduji schopnost myšice křovinné překonat vodní tok při hledání potravy, odchytem do pastí jsem zjistil, že z celkového počtu opakovaného odchytu jich vodní tok překonalo 20, z toho bylo 13 samic a 7 samců. Mohu se ptát, existuje rozdíl v míře bariérového efektu vodního toku mezi samci a samicemi? Očekávané hodnoty, proti nimž testuji mé měření jsou 10:10, protože předpokládám, že poměr mezi pohlavími je na lokalitě 50 % na 50 %.
• Příklad z přírodních věd 2: Ve vymezené oblasti byly sledovány tři asociace jednoho vegetačního svazu, jejich zastoupení na celkovém výskytu svazu v oblasti bylo 3:11:7. Liší se toto rozdělení četností od očekávaného poměru zastoupení 1:1:1?
• Příklad ze sociálních věd: v návštěvnosti zámku Kratochvíle jsem zjistil variabilitu v návštěvnosti podle věku návštěvníků. Mohu se ptát, odpovídá věková struktura návštěvnosti zámku Kratochvíle věkové struktuře obecné populace ČR? Poměr věkových kategorií zjistím z údajů ČSÚ.

Chí-kvadrát test používáme při testování souvislostí výskytu kombinací hodnot dvou proměnných = dvouvýběrový chí-kvadrát test

Základní informační shrnutí je na tabuli.

• Příklad z přírodních věd 1: U jistého druhu hlodavce v Arizoně byly identifikovány čtyři odstíny kožichu – tmavě hnědá, tmavě okrová, světle hnědá a světle okrová. Liší se zastoupení identifikovaných barev mezi pohlavími daného druhu hlodavce? Zastoupení měřených hodnot je následující: samice – 64:32:86:18; samci – 55:64:65:16.
• Příklad z přírodních věd 2: Liší se zastoupení druhově bohatých a druhově chudých lokalit ve třech vegetačních typech ve vymezeném území. Použijte soubor data1.xlsx, pro něj víme, že vegetační typ 2 patří do jednoho svazu a vegetační typ 2 do jiného svazu. (Budete muset slučovat kategorie a použít Yatesovu korekci.)
• Příklad z přírodních věd 3: Má barva samice vliv na to, jestli na ní jsou nebo nejsou zavěšeni při rozmnožování samci? Použijte soubor nominalni.xlsx a proměnné samice-barva a samci-ano.
• Příklad ze sociálních věd: Zámek Hluboká inovoval expozici trofejí třemi novými prvky a chce zjistit, jestli některá z těchto inovací ovlivnila spokojenost s návštěvou zámku a předpokládá, že spokojenost bude ovlivněna pohlavím (lovecké trofeje budou spíše doménou mužů než žen). Byl sestaven dotazník, kde měl každý z respondentů označit inovaci, se kterou je nejvíce spokojen a své pohlaví. Pak mohu testovat nulovou hypotézu: míra percepce atraktivnosti dílčích inovací je nezávislá na pohlaví návštěvníka.

V tomto případě použití nám “chybí” očekávané hodnoty – ty se pro každou buňku matice 1. proměnná versus 2. proměnná určí jako podíl součinu součtu četností daného řádku a součtu četností daného sloupce a celkového počtu pozorování (= vzorec je zeleně na předchozím obrázku).

V případě software STATISTICA je není nutné počítat, program to udělá sám – video.

Při výpočtech pamatujte na omezení chí-kvadrát testu, že žádná očekávaná četnost nesmí být nulová (nulou dělit nelze) a neměla by být menší než 1, což se běžně stává při měřených četnostech 0, a maximálně 20 % všech četností může být menších než 5 (žádná hodnota pod 5 u 2×2 tabulek). Pokud je menších četností více, je nutno použít Yatesovu korekci (červeně na předcházejícím obrázku), kterou se doporučuje provádět jen v 2 x 2 tabulkách.

K tomu, abyste mohli vypočítat chí-kvadrát s Yatesovou korekcí v MS Excel, budete muset znát funkci MS Excel ABS, která vrací absolutní hodnotu čísla nebo čísla vyjádřeného výrazem.

Videoprezentace

---

Fisherův exaktní test

Velkým problémem chí-kvadrát testu je to, že hodnota p je pouze odhadem, neboť rozdělení náhodného výběru nominálních dat je jen aproximací chí-kvadrát rozdělení. Tato aproximace je nespolehlivá u malých počtů měření a především v 2×2 kontingenčních tabulkách. Mám-li 2×2 kontingenční tabulku o malých četnostech, včetně nuly, pak se jako nejvhodnější varianta doporučuje použít Fisherův exaktní test. Testuje se nulová hypotéza, že rozdělení objektů podle dvou kritérií je odlišné od hypergeometrického rozdělení. Počítá se pouze hodnota p, kterou se testuje odlišnost sloupců od řádků. Vzorec pro výpočet je:

p = ((a+b)! (c+d)! (a+c)! (b+d)!)/(a! b! c! d! n!)

kde p je hladina významnosti, a, b, c, d jsou hodnoty v kontingenční tabulce v uspořádání SZ, SV, JZ, JV a n = a+b+c+d. Obrovskou výhodou je možnost použití tohoto testu, i když se některá z hodnot a,b,c,d rovná nule, neboť 0!=1.

V MS Excel je k výpočtu znát další funkci – FAKTORIÁL.

• Příklad z přírodních věd 1: Typické využití Fisherova exaktního testu je při testování společného výskytu dvou druhů při nízkém počtu měření. H0 zní, že neexistuje závislost ve výskytu dvou druhů. Navštívili jsme 15 náhodně vybraných lokalit a sledovali jsme výskyt dvou druhů ostřic, v 2×2 tabulce máme výskyt 6, 2, 1, 6, otázka zní, je výskyt těchto dvou druhů ostřic nezávislý? Řešení v MS Excel je na videu.
• Příklad z přírodních věd 2: Tímto testem testuji v JUICE koncentraci druhu v typu společenstva – musím mít definovány skupiny v základní tabulce (např. výsledek TWINSPANu, shlukové analýzy nebo ručně). Pak volím Synoptic Table a v něm Fidelity. Test si nastavím v Threshold Value na kartě Fidelity Measures, pak v Type . . . dávám phi coefficient a ve Standardisation . . . zaškrtrávám Calculate Fisher´s exact test.

Videoprezentace

RealStatistics podporuje Fisherovy exaktní testy v kontingenčních tabulkách 2×2 až 5×2 a 3×3.

---

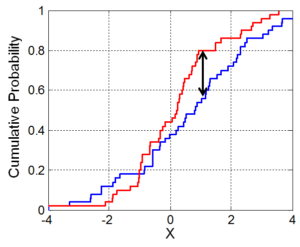
Kolmogorov-Smirnov test

Jde o alternativu chí-kvadrát testu. Testují se v něm rozdíly mezi výběry (dvouvýběrový) nebo výběrem a teoretickým rozdělením (jednovýběrový test dobré shody) v relativních kumulativních četnostech (absolutní hodnota rozdílu). Největší rozdíl je pak testovacím kritériem, které je posuzováno oproti tabelované kritické hodnotě pro odpovídající hladinu významnosti a počet stupňů volnosti (d.f. = počet měření (n)).

Videoprezentace

Jednovýběrový Kolmogorov-Smirnov test se nejčastěji používá k testování shody rozložení dat s teoretickým rozdělením, nejčastěji normálním.

Výpočet K-S testu v MS Excel je na videu.

Výhodou Kolmogorov-Smirnov testu je jeho neomezení počtem četností výskytu v očekávaných hodnotách méně než 5, a tak ho lze využít jako alternativu, kde není možno použít chí-kvadrát test, nicméně stále platí, že v žádné skupině nesmí být 0.

---

Z-test

Pokud z nějakého důvodu potřebujete testovat poměry a nikoliv četnosti, tak nemůžete použít chí-kvadrát test (který asi jako první nabízí), protože velikost souboru ovlivňuje kritickou hodnotu chí-kvadrát testu a je tedy rozdíl jestli jste v pokusu měli 10, 25 100, nebo 2500 objektů a převodem na procentický poměr byste všechny výše uvedené četnosti převedli na 100.

V případech nutnosti testování poměrů se požívá z-test, který není předmětem naší výuky a návod na jeho výpočet najdete v učebnici R jako kapitolu Advanced R3.

Videoprezentace

---

Vizualizace nominálních dat

Četnosti jsme se naučili vizualizovat pomocí histogramu, kromě něj můžeme použít klasické koláčové grafy a nejvhodnější je vizualizace pomocí mozaikových grafů (mosaicplots). Návod pro R včetně videa najdete v sedmé lekci R.

---

ORDINÁLNÍ DATA (8. lekce R)

Další zde uvedené testy jsou určeny pro ordinální data a založeny jsou na porovnávání pořadí.

MS Excel je schopen přiřadit pořadí hodnotám funkcí, která se jmenuje rank. Zde nezapomínejte používat opravný faktor, jehož hodnotu musíte přičíst k hodnotě získané funkcí rank – je to nutné, pač ve Vašich datech může být jedna hodnota vícekrát a funkce rank jim všem přiřadí nejmenší hodnotu pořadí, což je pro tyto metody špatně – tam musíte mít v těchto případech průměrnou hodnotu pořadí těchto čísel.

Videoprezentace

---

Mann-Whitney test

Testujeme shodu rozdělení jedné měřené proměnné u dvou provedených výběrů. Jde o základní test sloužící k porovnání dvou výběrů (= jde o ordinální obdobu dvouvýběrového t-testu). Test vychází z pořadí a počtu měření. Základní informační shrnutí je na tabuli.

• Příklad z přírodních věd 1: Měřili jsme pH na dvou typech stanovišť rašeliništní vegetace nejmenované oblasti. Chceme zjistit, jestli se liší hodnoty pH mezi vegetacemi druhově bohatými a druhově chudými. Příprava dat pro výpočet v MS Excel je na videu a na tomto videu je vlastní výpočet testu.
• Příklad z přírodních věd 2: Měřili jsme koncentraci Ca2+ iontů na dvou typech stanovišť rašeliništní vegetace nejmenované oblasti. Chceme zjistit, jestli se liší hodnoty koncentrace Ca2+ iontů mezi vegetacemi druhově bohatými a druhově chudými. Použijte stejný soubor jako v příkladu předchozím.
• Příklad z přírodních věd 3: Pro brusnici brusinku byla sledována míra konkurenceschopnosti na jižních a severních svazích při horských hřebenech – sledována byla pokryvnost druhu na 20 plochách 1 x 1 metr na svazích s jižní a severní expozicí, nulová hypotéza zní – Podmínky svahu jižní a severní expozice neovlivňují pokryvnost brusnice brusinky při horských hřebenech.
• Příklad ze společenských věd: chci zjistit, jestli se v České republice liší návštěvnost zámků a hradů – z NIPOS získám informace o návštěvnosti hradů a zámků pro ČR např. za rok 2012 a provedu test nulové hypotézy – návštěvnost hradů a zámků v ČR se neliší.

Videoprezentace

---

POZOR!!!

Vzhledem k tomu, že U je definována jako jakákoliv hodnota, která má být malá, když platí H1, tak jsou statisticky významné hodnoty testovacího kritéria nižší než daná kritická hodnota.
Lze brát nižší hodnotu U nebo (jak je uvedeno v učebnici) vyšší hodnotu U – pro oba postupy se tabulky liší.
Pro jednostranný test záleží na tom, jestli řadíte hodnoty od nejvyšší k nejmenší, nebo je řadíme od nejmenší k největší.

Srovnat lze i větší počet nezávislých výběrů, test se jmenuje Kruskal-Wallisův test (viz zde dole).

Wilcoxonův test

Používá se pro testování párových dat – jedna měřená proměnná u jednoho výběru, kde je každý objekt (jedinec, …) měřen dvakrát. Test je založen na pořadí rozdílů jednotlivých měření (= jde o ordinální obdobu párového t-testu). Základní informační shrnutí je na tabuli.

• Příklad z přírodních věd 1: Na rašeliništích jsme měřili pH podzemní vody na jaře a v létě. Existuje rozdíl mezi jarním a letním měřením? Řešení v MS Excel je na videu.
• Příklad z přírodních věd 2: Na stejných lokalitách jako pH jsme měřili na jaře a v létě konduktivitu. Existuje rozdíl mezi jarním a letním měřením? Použijte stejný soubor jako v předchozím příkladu.
• Příklad ze společenských věd 1: Má návštěva turistického místa vliv na percepci jeho zajímavosti? Návštěvníci mají před návštěvou rozhodnout o míře zajímavosti určitého místa, následně toto místo navštíví a s odstupem času po návratu se osloví stejným dotazem jako před odjezdem. Podmínkou je zajištění možnosti spárování odpovědí před odjezdem a po návratu.
• Příklad ze společenských věd 2: Existují rozdíly v odměňování personálu hotelů podle příslušnosti k české a ukrajinské národnosti. Podmínkou provedení testu je získání informací o výši odměny vyplácená českým a ukrajinským pracovnicím v hotelu – párují se informace za hotel.

Videoprezentace

Srovnat lze i větší počet závislých výběrů, test se jmenuje Friedmanova ANOVA – k ní se však dostaneme až v navazujícím kurzu, jinak je tady dole.

Na tomto místě se podíváme na základní parametrické metody pro jeden a dva výběry – těmi jsou t-test a F-test. Definovány jsou, jak bylo zmíněno dříve, na poměrových datech a předpokladem jejich použití je normalita dat. Testovanými parametry jsou průměr (t-test) s využitím střední chyby průměru a rozptyl (F-test). Výpočty všech těchto parametrů jsme řešili dříve.

T-test = testování průměrů

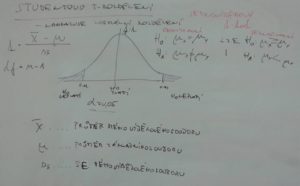
V praktické statistice se normální rozdělení nahrazuje t-rozdělením, které je mu velmi podobné. Jeho charakteristiky umožňují testovat hypotézy, které jsou vázány na průměr. Ty nás zajímají nejčastěji, a proto patří metody testování založené na tomto rozdělení k nejvýznamnějším základním testovacím metodám pro dva výběrové soubory. Nicméně v podstatě můžeme rozlišit tři typy možností nulových hypotéz, které obvykle testujeme různými t-testy.

T-test = testování průměrů

V praktické statistice se normální rozdělení nahrazuje t-rozdělením, které je mu velmi podobné. Jeho charakteristiky umožňují testovat hypotézy, které jsou vázány na průměr. Ty nás zajímají nejčastěji, a proto patří metody testování založené na tomto rozdělení k nejvýznamnějším základním testovacím metodám pro dva výběrové soubory. Nicméně v podstatě můžeme rozlišit tři typy možností nulových hypotéz, které obvykle testujeme různými t-testy.

Jednovýběrový t-test

Průměr proměnné z dat získaných našim měřením se testuje oproti průměru teoretickému (= očekávanému průměru či známému průměru základního souboru), jímž může být např. hodnota uváděná v literatuře. Tohoto testu používáme např. při srovnávání výsledků našeho výzkumu s výzkumem předchozím.
Podstatou testu je podíl dvou hodnot – v čitateli je rozdíl průměru našich hodnot a teoretického průměru (který jsem našel např. v literatuře – třeba v Květeně ČR), ve jmenovateli je střední chyba průměru vypočítaná z našich dat. Výpočet průměru a jeho střední chyby jsme si ukázali v sekci charakteristiky dat. Všechny výpočty jsou uvedeny na tabuli a vlastní postup uvažování jsme si představili, když jsme si představovali princip testování hypotéz.

Jednovýběrový t-test.

Výpočet jednovýběrového t-testu v R naleznete v šesté lekci R.

• Příklad z přírodních věd 1: Na náhodně vybraných lokalitách podle druhového složení definovaného typu rašelinišť jsme měřili reakci půdy. Liší se průměrná hodnota reakce půdy na mnou měřených lokalitách daného typu rašeliniště od v literatuře uváděné průměrné hodnoty reakce půdy stanovišť těchto rašelinišť, která je 3,9? Data jsou v souboru data1.xlsx, proměnná pH1, typ rašeliniště v proměnné typ=2.
• Příklad z přírodních věd 2: V našem výzkumu jsme zjistili, že průměrná hodnota konduktivity podzemní vody na lokalitách s výskytem Dactylorhiza trausteineri je 54 a srovnávám tuto hodnotu s hodnotou uváděnou v literatuře pro tento druh. Tento test použiji, protože nemám k dispozici jiný údaj než je hodnota průměru. Pokud je v literatuře uveden i počet n a velikost směrodatné odchylky (což by být mělo, jak jsme si říkali v úvodu), pak použiji dvouvýběrové varianty t-testu.
• Příklad ze společenských věd: V našem výzkumu jsme zjistili, že průměrná známka hodnocení přitažlivosti expozice zbraní na jistém zámku je 4,12 (hodnoceno na škále 1 až 9) a srovnávám tuto hodnotu s hodnotou přitažlivosti expozice zbraní uváděné v literatuře pro zámky v Bavorsku (předpokladem, že bylo použito stejné škály hodnocení). Tento test použiji, protože nemám k dispozici jiný údaj než je hodnota průměru. Pokud je v literatuře uveden i počet n a velikost směrodatné odchylky (což by být mělo, jak jsme si říkali v úvodu), pak použiji dvouvýběrové varianty t-testu.

Párový t-test

Platí, že máme už dvě měření (na rozdíl od předchozí statistiky), ale obě měření nejsou vzájemně nezávislá – obvykle jde o dvoje měření na jednom objektu – je samozřejmé, že jde o měření jedné náhodné veličiny. Používá se např. při testování změny měřeného jevu na jedinci. Do testu ale v tomto případě nevstupují obě měření jako dva výběry, ale od jednoho měření (obvykle druhého) odečtu hodnotu druhého měření (obvykle se jedná o hodnoty z prvního měření). Pokud nedošlo ke změně mezi měřeními, pak by se tento rozdíl měl rovnat nule. Testuje se, jestli tomu tak opravdu je, tedy testuje se rozdíl měření (hodnoty rozdílu obou měření) oproti očekávanému průměru, jímž je v tomto případě 0 (tedy mí = 0). Vše podstatné je na tabuli.

Podstata párového t-testu.

Výpočet pérového t-testu v R naleznete v šesté lekci R.

• Příklad z přírodních věd: Zajímá mě, jestli záleží na tom, kdy měřím množství živin v substrátu (= podzemní vodě) na výzkumných plochách. Provedl jsem na každé ploše měření amoniakálního dusíku na jaře a na podzim. Testuji, jestli se rozdíl měření na každé ploše rovná nule (pokud není rozdíl v měření, pak se na každé ploše musí rovnat rozdíl jarního a podzimního měření nule). Na výpočtu tohoto příkladu se naučíme pracovat s Analytickými nástroji MS Excel – video.

Výpočet párového t-testu v MS Excel pomocí analytických nástrojů.

• Příklad ze společenských věd: Testuji vliv návštěvy expozice historických zbraní na znalost návštěvníků. Před návštěvou dostanou návštěvníci deset úkolů, za správně zodpovězený úkol dostanou bod – a získají tak nějaký počet bodů. Po ukončení návštěvy dostanou stejné otázky a opět je jim sečtou body. Od bodů získaných po návštěvě odečteme body získané před návštěvou a testujeme jestli je jejich rozdíl nezvýšil – zde půjde o jednostranný test, H0 tedy je mí je rovno nebo je větší než 0.

Prozatím jen na okraj zmiňme, že v praxi takové výzkumy zas až tak jednoduché nejsou, protože nevíme, co vše může být příčinnou změny – pokus je třeba vždy plánovat a obvykle je třeba mít nějakou kontrolní skupinu, kde nedošlo k žádnému zásahu. Navíc, pokud testuji rozdíly mezi dvěma skupinami, tak bychom měli nejprve vypočítat rozdíly v každé skupině a teprve tyto dva rozdíly testovat dvouvýběrovým t-testem, nebo vybrat jinou sofistikovanější metodu z těch, které budeme řešit v navazujícím studiu např. zde nebo v některých případech i zde.

Dvouvýběrový t-test

Měřím jednu proměnnou ve dvou výběrech a testuji, jestli se neliší průměry těchto dvou výběrů. Oba výběry jsou na rozdíl od předchozího testu nezávislé. Kromě normality je dalším požadavkem, aby oba výběry měly stejnou varianci. Vzorec pro výpočet testu je odvozen od vzorce pro výpočet jednovýběrového t-testu. V čitateli je v tomto případě ale rozdíl průměrů obou výběrových souborů, ve jmenovateli je pak střední chyba průměru rozdílu obou průměrů. Výpočet této střední chyby je komplikovaný a vychází z podílů odhadované společné variance obou výběrů. Počet stupňů volnosti se pak rovná součtu počtu měření v obou výběrech sníženém o 2. Vše podstatné je shrnuto na tabuli.

Dvouvýběrový t-test.

Pokud je soubor měření dostatečně velký, tak není porušení pravidla stejné variance nijak zásadní. Pokud je soubor malý a variance diametrálně odlišná, pak se počítá “přibližné t” s přibližným počtem stupňů volnosti. Oba výpočty umí přes Analýzu dat MS Excel vypočítat. My však pro výpočet dvouvýběrového t-testu použijeme R v šesté lekci R.

• Příklad z přírodních věd 1: Měřil jsem reakci substrátu na jednot typu biotopu (rašeliniště) v geograficky uzavřené oblasti. Ze základního souboru druhově bohatých a druhově chudých rašelinišť byly vybrány náhodně lokality výzkumu. Zajímá mě jestli se liší průměrné hodnoty reakce půdy mezi stanovišti druhově bohatých a druhově chudých rašelinišť Vzhledem k náhodnosti výběru, předpokládané normalitě obou výběrů a nezávislosti obou výběrů, mohu požít dvouvýběrového t-testu – video pro řešení v MS Excel s pomocí Analytických nástrojů.

Výpočet dvouvýběrového t-testu v MS Excel.

• Příklad z přírodních věd 2: Sleduji reakci změn v růstu rdestu vzplývavého na použití vápence a dolomitu při vápnění rybníků. V pokusných nádobách změřím velikost jedinců, pak aplikuji na část vápenec a na část dolomit, po uplynutí stanovené doby změřím opět všechny jedince, zjistím pro každý rozdíl v přírůstcích a t-testem testuji rozdíl v průměrných přírůstcích mezi jedinci na něž byl aplikován vápenec a jedinci, na něž byl aplikován dolomit.
• Příklad ze společenských věd: Liší se spokojenost s návštěvou turistické atraktivity mezi muži a ženami? Spokojenost je měřena na škále hodnot např. 1-5, předpokládám spojitost dat ve významu pro návštěvníka a zajistil jsem náhodným výběrem respondentů “normalitu” dat v odpovědích.

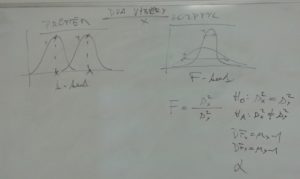
F-test = test rozptylu

F-test je dvouvýběrovým testem, kterým se testuje shoda rozptylů těchto dvou výběrů. Používá se ve stejných případech, jako dvouvýběrový t-test. Rozdíl je v tom, že u t-testu se ptám po případné existenci rozdílu v průměru, ale u F-testu se ptám po případné existenci rozdílu ve variabilitě dvou výběrů.

Základní informace k testu jsou shrnuty na tabuli – jen doplňme, že v čitateli je obvykle hodnota rozptylu, která je větší – výsledkem je tak hodnota větší než 1. Existují ale i tabulky, které počítají s vyšší hodnotou ve jmenovateli – pak ale nulovou hypotézu zamítáme, když je hodnota testovacího kritéria menší než hodnota kritická. MS Excel je schopen spočítat obě varianty zadání vstupních dat (vstupní data vypadají stejně jako vstupní data pro párový t-test).

Výpočet F-testu v R naleznete v šesté lekci R.

F-test a jeho srovnání s t-testem.

Vlastní F-test obvykle používáme méně často než t-test (průměry nás zajímají obvykle častěji než variance), přesto v ekologii má variabilita stejně velký význam jako vlastní střední hodnota proměnné.

Nicméně význam F-testu je na úrovni našeho základního studia extrémní, pač F-test je podstatou porovnávání více než dvou výběrů v testu se jménem ANOVA (analýza rozptylu) – zde nahoře – a při testování lineárních regresních modelů.

POZOR!!!!! – mám-li více výběrů než dva (např. nemám samce a samice, ale mám čedič, vápenec a žulu), nemohu řetězit dvouvýběrové t-testy ani F-testy, ale musím použít metodu ANOVA. K tomu se ale ve výuce dostaneme až po přehledu neparametrických metod.

Shrnutí

Všechny proměnné, které měříme, jsou náhodnými veličinami, . . . co to znamená? 

Veličinu chápeme jako vyjádření výsledku měření výskytu nějaké charakteristiky (označované jako znak) nějakého jevu vázaného na objekt mého výzkumu. Problémem je, že všechna měření všech znaků charakteristických pro všechny jevy jsou vždy ovlivněny spoustou faktorů, které měřit nejsem schopen, ani při největší snaze. Tyto faktory mají za následek, že veličina pak ze své podstaty nemůže být nikdy změřena absolutně správně. Za různých konstelací neměřitelných a nesledovatelných podmínek pak může mé měření dopadnout různě. To je důvod, proč se měřené veličiny označují jako veličiny náhodné.

Pravděpodobnost

Z výše uvedeného plyne, že to, co konkrétně změřím, je pouze konkrétní realizace (daná v podstatě náhodou) této náhodně měřené veličiny z nekonečně velkého potenciálně možného počtu veličin. My jsme si toho vědomi a tak víme, že to, co jsme aktuálně změřili, je pouhou jednou variantou z obvykle nekonečného množství teoreticky změřitelných hodnot – měření mohu opakovat tolikrát, kolik my zbývá sil, a pokaždé změřím něco (trošku) jiného. Předpokládám ale, že různé konkrétní hodnoty mohu změřit s různou pravděpodobností. Jinak řečeno, určité hodnoty mohou být naměřeny častěji než hodnoty jiné.

Každá náhodná veličina tak má své rozdělení pravděpodobností měření konkrétních hodnot. Každá konkrétní hodnota je tak charakteristická pravděpodobností, že bude její hodnota změřena. Tuto skutečnost je pak teoreticky možné vyjádřit funkcí hustoty pravděpodobnosti, jež se často vyjadřuje grafem, který, vulgárně řečeno, vypadá jako funkční spojité vyjádření histogramu – na ose x jsou jednotlivé konkrétní hodnoty náhodné veličiny a na ose y je pak míra pravděpodobnosti výskytu takového hodnoty (vyjádřená v hodnotě funkce hustoty pravděpodobnosti). Plocha pod touto křivkou se pak rovná 100% pravděpodobnosti změření všech hodnot proměnné.

Distribuční funkce

Dalším typem vyjádření pravděpodobnosti výskytu hodnoty náhodné veličiny je distribuční funkce pro libovolnou měřenou hodnotu, která udává pravděpodobnost, že reálně měřená hodnota bude menší než hodnota libovolně stanovená. Hustota pravděpodobnosti je derivací distribuční funkce.

Přesnost odhadu

Pokud nepředpokládáme existenci světa o sobě (jak jsou něm přesvědčeni např. Platón a Kant), pak průměr základního souboru není náhodnou veličinou – je konečný a Božsky správný. Nicméně stále platí, že průměr z náhodného výběrového souboru náhodnou veličinou je – teoreticky lze ze základního souboru udělat nekonečně mnoho náhodných výběrů a průměry těchto jednotlivých náhodných výběrů se budou lišit – tabule. V logice tohoto uvažování mohu kromě variability průměru jednoho náhodného výběru (dané směrodatnou odchylkou tohoto průměru) identifikovat také variabilitu průměru z průměrů. Tuto variabilitu nemusím ale počítat z nekonečného množství náhodných výběrů z daného základního souboru, ale mohu ji odhadnout na základě rozptylu a počtu měření, ze kterých byl průměr vypočítán. Tato hodnota se vypočítá jako odmocnina z podílu rozptylu a počtu měření – jde o hodnotu přesnosti odhadu průměru výběrového souboru = střední chyba průměru, nejčastěji se značí S.E. (z anglického standard error of mean). Vedle směrodatné odchylky je střední chyba průměru druhou nejdůležitější charakteristikou variability průměru, tentokrát ale nikoliv ve vztahu k vlastním měřeným datům (jak je tomu u směrodatné odchylky) ale k průměru základního souboru – všimněte si ve vzorci, že je závislá na počtu měření – čím je počet měření větší, tím je menší S.E. při stejné hodnotě průměru i směrodatné odchylky. V R je třeba aktivovat package sciplot a v něm je to funkce se(). V MS Excel se při výpočtu S.E. lze naučit používat dříve zmíněnou funkci MS Excel – POČET – která vrátí počet buněk v poli dat a je v podstatě zjednodušenou variantou dříve poznané funkce ČETNOSTI. Taktéž si ukážeme možnosti použití více funkci a vkládání funkcí do funkcí na příkladu výpočtu střední chyby průměru = SMODCH.VÝBĚR(A2:A22)/ODMOCNINA(POČET(A2:22)), další poznanou funkcí tak bude ODMOCNINA.

Třetí charakteristikou variability průměru jsou pak konfidenční intervaly spolehlivosti průměru. Jde o interval v němž s nějakou mírou pravděpodobnosti průměr leží. Průměr sám je samozřejmě bodovým odhadem, ale už z S.D. je jasné, že data mají jistou variabilitu a všechny měřené hodnoty nemají obvykle hodnotu průměru. S ohledem na počet měření jsem pak schopen identifikovat míru pravděpodobnosti, ve které průměr “opravdu” leží. Obvykle se udává interval 95% – jde o interval, ve kterém s 95% pravděpodobností průměr leží (nejde tedy o bod, ale o interval hodnot). Vypočítá se jako hodnota průměru plus/mínus kritická hodnota testovacího kritéria pro hladinu významnosti alfa = 0,05 (najdeme ji u t-testu a je rozdílná pro rozdílné počty měření, potažmo stupně volnosti – k tomuto najdete vysvětlení u testování hypotéz).